Uh-oh, just lost half the audience at the title! Don’t despair, you needn’t be an engineer to do the simple calculations we all encounter in ham radio, sooner or later. This article lists some resources and shows you how to do some basic calculations correctly and with the right tools. Once you are comfortable with these, other problems will be easier. So sharpen up your Number 2 or run that calculator app and let’s get math-y!
If you need a math class refresher, here is a long list of online math tutorials from the ARRL. The Paul’s Math Tutorials website is another resource.
A resource available to anyone reading this article is the calculator built in to your PC or phone’s operating system. For Windows, you’ll find it in the Accessories group. I “pinned” it to my command bar so it’s available with a single click all the time.
Windows calculator:
Macintosh calculator:
Android calculator:
iOS calculator:
This article is based on the Windows calculator shown above, but all of the calculators have similar functions. Online calculators abound, available via your browser.
Start by setting your calculator to perform “Scientific” functions. Then set its default angle to degrees; the choices in Windows are DEG (degrees), RAD (radians), and GRAD (grads). Finally, find out how to access the trigonometry or “trig” functions for angles. They are accessed through the TRIG button on the Windows calculator.
Your calculator may have buttons pre-programmed with the values for pi (3.14159, represented by the Greek letter π ) and e (2.71828). You’ll encounter pi in quite a few formulas, such as for reactance. Euler’s number, e, is used when calculating time constants of RC and RL circuits. Another common value in electronic equations is 2 x pi = 2 π = 6.28318. Nearly every calculation only needs a couple of decimal places, so treat pi as 3.14, 2 x pi or 2 π as 6.28, and e as 2.72 π .
Conversions
Let’s start with converting one type of unit to another. For example, to convert inches to feet, divide by 12. You may be surprised to learn that the Windows calculator has unit conversions built in! In the same menu you used to set your calculator to its “Scientific” mode, there is a group of Conversions at the bottom. Select the type of conversion and a whole new calculator window appears. Select the units you have and enter the quantity. You’ll see the converted value below and you can select the units that you want. Try converting a pound of diamonds to carats!
If you find yourself without a built-in calculator, most browsers will perform conversions, too—just enter “convert [first unit] to [second unit]” and a window or online calculator will appear.
One set of conversions your calculator probably won’t have are the conversions between ac voltage measurements. A sine wave can be measured in terms of its instantaneous value at any time, but the most useful are peak-to-peak, peak, and RMS (root-mean-square) values as shown in the following graphic from Chapter 3 of the ARRL Handbook.

While some multimeters can measure voltages in all three ways, most make RMS measurements. Here’s how to convert between them. Remember that these conversions only work for sine waves.
| To convert | to | Multiply by |
| RMS | Peak-to-Peak | 2.828 |
| RMS | Peak | 1.414 |
| Peak | Peak-to-Peak | 2 |
| Peak | RMS | 0.707 |
| Peak-to-Peak | Peak | 0.5 |
| Peak-to-Peak | RMS | 0.354 |
Example: What is the peak voltage a capacitor must withstand if it is connected across the 120V ac line voltage? Since household ac voltages are an RMS value, multiply 120 x 1.414 = 169.9 V. Use a capacitor rated at 200 V at a minimum!
Ohm’s law and Power Equation
No discussion of math in electronics would be complete without Ohm’s law and its close cousin, the power equation. If you are comfortable with basic algebra, all you have to remember is one form of Ohm’s law and of the power calculation. You can work out the rest from there. If you prefer visual aids, the most common aid is the Ohm’s law triangle shown below.
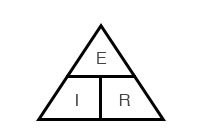
The basic form of Ohm’s Law is R = E / I, where E is the symbol for electromotive force or EMF. EMF is also known as voltage and the symbol for voltage is V, so you might see it written as R = V / I. Just remember that E and V are equivalent.
To use the triangle, place your finger on the value you want to calculate (E, I, or R) and the triangle shows you the calculation you need to make. For example, placing your finger on R leaves E above I so divide voltage by current. The three equations are:
- R = E / I
- E = I x R
- I = E / R
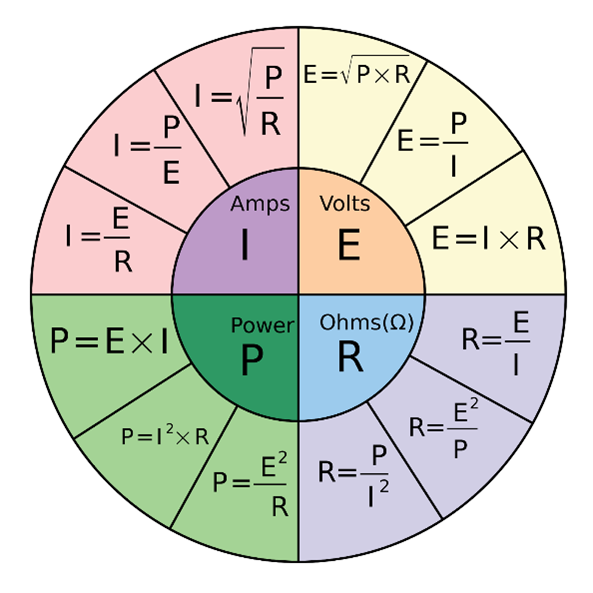
Power is calculated in much the same way: P = E x I or V x I. Like Ohm’s law it has two other forms: E = P / I and I = P / E. You can also substitute the Ohm’s law equations for E or I into the power equations and come up with forms like P = E2 / R. The wheel below contains all of the basic equations showing three ways to calculate P, E, I, and R. No matter which of the two values you know of those four, you can calculate the other two.
Using Ohm’s Law to Choose Wire Size
How about a practical use of Ohm’s law? Let’s say you are installing a new mobile radio that draws 20 amps on transmit. What size wire do you use so the resistance of a 10-foot power cable doesn’t create a voltage drop larger than 0.5 V?
Start with the two things you know—voltage (0.5 V) and current (20 A)—and use them to calculate the maximum allowed resistance: R = V / I = 0.5 V / 20 A = 0.025 Ω . Remember that there are 2 x 10 feet = 20 feet of wire in that two-conductor cable!
The next step is to find out what gauge of wire you need so that 20 feet of it will have 0.025 Ω or less. You can find copper wire tables in Chapter 22 of the ARRL Handbook, or online at RF Cafe. The table will tell you the resistance of each gauge for 1000 feet of wire. To convert the 0.025 Ω for 20 feet of wire to the resistance for 1000 feet, multiply it by 1000 / 20 = 50. The smallest gauge of wire you can use will have a resistance of 50 x 0.025 = 1.25
Ω per 1000 feet. Looking at the table, #10 is the smallest gauge with a resistance lower than 1.25 π /1000 feet. (#12 has 1.62 Ω /1000 ft.) Summarizing the three basic steps:
- Calculate maximum resistance = voltage drop / current drawn
- Calculate maximum resistance per 1000 ft. = maximum resistance ´ (1000 ft. / wire length in ft.)
- Find the smallest gauge with a smaller value of resistance per 1000 ft.
Math pro tip: When you see something in parentheses, like the (1000 ft. /wire length in ft.) above, calculate that first!
Here are two other related questions that you might have to answer when installing radios or power supplies:
How much voltage drop will occur in a certain gauge and length of wire for a given amount of current?
- From the table, determine resistance per 1000 ft. of that gauge wire.
- Multiply that value by the wire length / 1000 to find the resistance of the wire. (Remember that for two-conductor cables, total length is twice the cable length!)
- Voltage drop = wire resistance ´ current
Example: For 25 feet of #16 wire, what is the voltage drop at 5 A? From the table, #16 wire has a resistance of 4.09 Ω / 1000 ft. The 25 feet of wire will have a resistance of 4.09 x (25 / 1000) = 0.102 Ω . The voltage drop = 0.102 x 5 = 0.512 V.
How much current can be drawn through a wire of a given gauge and length without exceeding a maximum voltage drop?
- Find the wire’s resistance = resistance per 1000 ft. from the table ´ (length / 1000).
- Calculate the maximum current = voltage drop / wire resistance.
Example: How much current can flow through #12 wire, 10 feet long, with a maximum drop of 0.1 V? #12 wire has 1.62 Ω /1000 ft., so this length of wire has a resistance of 1.62 x (10 / 1000) = 0.0162 ohms. Maximum current = 0.1 V drop / 0.0162 Ω = 6.18 A.
Reactance and Impedance
Let’s have a piece of that pi, shall we? You will use pi when calculating a value of reactance. Reactance, abbreviated X, is the opposition to ac current flow by a capacitor or inductor. The reactance of an inductor, XL, is positive, and of a capacitor, XC, is negative. Reactance changes with frequency, f, so you have to include that in the calculations, too. Frequency is in hertz (Hz), capacitance is in farads (F), and inductance is in henrys (H).
- XC = 1 / 2 π f C
- XL = 2 π f L
Math pro tip: Radio electronics deals with values much smaller than a farad or henry and much larger than a hertz. This would be a great time to practice using scientific notation (value x 10EXPONENT) on your calculator! (There are tutorials on the metric system and scientific and engineering notations in the math resources listed at the start of this article.)
Example: What is the reactance of a 100 pF capacitor at 20 MHz?
XC = 1 / (2 x 3.14 x 20 MHz x 100 pF)
= 1 / (6.28 x 20 x 106 Hz x 100 x 10-12 F)
= 1 / (0.0124)
= 79.6 Ω
Calculator pro tip: Calculate the bottom, or denominator, of the fraction first (the 2 π fC part) and then use the “1/x” key to do the division.
Example: What is the reactance of a 47 nH inductor at 50 MHz?
XL = 2 x 3.14 x 50 MHz x 47 nH
= 6.28 x 50 x 106 x 47 x 10-9
= 14.7 Ω
You can also turn these equations around and ask, “How many pF or nH do I need to get a certain amount of reactance?” This question gets asked when trying to match an antenna or build a filter.
- C = 1 / 2 π f XC
- L = XL / 2 π f
Example: How much capacitance has a reactance of 150 ohms at 146 MHz?
C = 1 / (6.28 x 146 x 106 x 150)
= 1 / (1.37 x 1011)
= 7.27 x 10-12 = 7.27 pF
Example: How much inductance has a reactance of 300 ohms at 7 MHz?
L = 300 / (6.28 x 7 x 106)
= 6.82 x 10-6 = 6.82 mH
Electronics pro tip: You may encounter the Greek letter Θ in some electronics books and articles. This symbol represents another way of expressing frequency, called angular frequency, which is equal to 2πf.
The Decibel
A very common calculation in ham radio is the decibel, abbreviated dB, which is spoken “deebee.” (Note the B is capitalized). Rather than go through the whole explanation of decibels here, you can read my QST article “Untangling the Decibel Dilemma.” That article has lots of background on calculating dB and some examples to guide you. What we need to review here is how to use a calculator to handle the logarithm calculations.
On your calculator, find the key labeled “log.”
To calculate a decibel value, first calculate the ratio you’re going to convert to dB. Then press “log.” Then multiply that value by 10 if the ratio is of two powers and by 20 if the ratio is of two voltages.
Example: What is the gain of an amplifier that outputs 25 watts with an input of 3 watts? First, calculate the power ratio of 25 / 3 = 8.33. Then press “log”: the log of 8.33 = 0.921. Then multiply by 10 = 10 x 0.921 = 9.21 dB.
Math pro tip: Don’t use the “ln” key! It’s a different type of logarithm based on powers of e instead of powers of 10.
Example: How much does a filter attenuate a signal if the input is 1.5 V and the output is 0.2 V? First, calculate the voltage ratio of 0.2 / 1.5 = 0.133. Then press “log”: the log of 0.133 = -0.875. Then multiply by 20 = 20 x -0.875 = -17.5 dB. Since a negative value represents attenuation, our filter attenuates the input signal by 17.5 dB. In other words, the filter’s “gain” is -17.5 dB.
Math pro tip: When calculating the dB equivalent of a voltage ratio, both voltages must be measured across the same value of impedance. In our example, the filter must have a load connected to its output that is the same value as its input impedance.
Finally, how do you get back to a ratio from dB? That’s where the “10x” key comes in! (On some calculators, the same function may have a key labeled “log-1” or you may have to press “INV” before “log.” Starting with the dB value, to convert back to a power ratio, divide by 10. Then press the “10x” key to “un-log-i-fy” and recover the ratio.
Example: What is the power ratio for 13 dB? First, divide 13 by 10 = 1.3. Next press “10x” to get 19.95 which is approximately 20.
Example: What is the voltage ratio for -27 dB? First, divide -27 by 20 since we are working with voltage: -27 / 20 = -1.35. Pressing “10x” gives us the voltage ratio of 0.45.
Math pro tip: A negative value of dB means the ratio is less than 1.
Angles
Finally (I can hear that sigh of relief!), you should check out the trigonometry or “trig” functions of the calculator. Push that “Trigonometry” button on the Windows calculator and you will see the basic functions “sin” (sine), “cos” (cosine), and “tan” (tangent). If you press the “2nd” button, those functions will turn into their “inverse” functions of sin-1, cos-1, and tan-1. Don’t forget there is a trigonometry tutorial listed at the beginning of the article!
Before we calculate anything, be sure your calculator shows “DEG” above the “Trigonometry” button. That means all angles will be entered, calculated, and displayed in degrees. The other options are radians and grads which are more useful in different types of calculations. Angles are usually represented by the Greek letter theta, θ .
The way to calculate a trig function is to enter an angle (in degrees, remember), press the “Trigonometry” button, then the button for the function you want.
Example: What is the tangent of 30 degrees? Enter 30, then press “Trigonometry” and select “tan” to get 0.577.
You can also “go backwards” as with log calculations in dB by using an inverse function. Those functions answer questions like, “What angle gives me this value of the sine function?”
Example: What angle results in a value for sine of 0.8? Enter 0.8, then press “Trigonometry” and select “sin-1” to get 53.1 degrees.
Trig pro tip: Angles given by inverse trig functions on calculators will be between +90 and -90 degrees, even though there are larger angles that will give the same answer. Most problems that involve trig don’t involve the larger angles, anyway.
Here are a couple of situations in which a ham can make good use of trig:
How long is a guy wire without having to take it off a tower? Measure the distance from the guy anchor to the base of tower. Then use a protractor to sight along the guy wire and find the angle, θ , it makes with the ground (90 degrees is vertical and 0 degrees is horizontal). The guy wire’s length = distance to tower / cos ( θ ).
Example: From the anchor, 60 feet from the base of the tower, the guy makes an angle of 50 degrees with the ground. Guy wire length = 60 / cos(50) = 60 / 0.0107 = 93.3 feet. (Practically speaking, the minor sag of a taut guy wire will have a negligible effect on this calculation.)
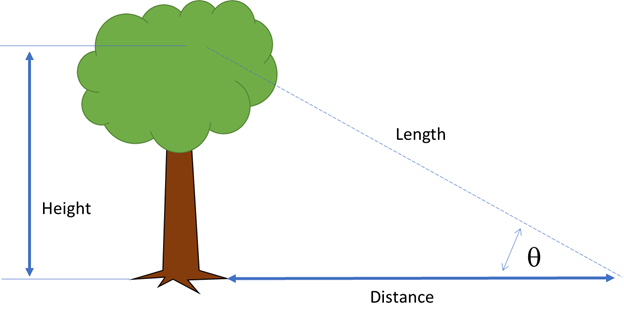
How far from the base of a tree of a known height will the end of your wire antenna reach the ground? Figure the angle the antenna will make with the ground: θ = sin-1 (tree height / antenna length). Then calculate how far the antenna will reach from the tree = antenna length x cos( θ).
Example: If I have a pulley in a tree at 60 feet, will a 135-foot 80 meter dipole fit if my yard ends 100 feet from the tree? Start by calculating the angle to the edge of the yard: θ = sin-1(60 / 135) = sin-1(0.444) = 26.4 degrees. The space I need is 135 x cos(26.4) = 135 x 0.895 = 121 feet. No, the antenna won’t fit!
How high is a tower without climbing it? Move away from the tower until the angle from your eyes to the top of the tower is between 30 and 60 degrees (that range will give you reasonably accurate results). Calculate distance from tower base x tan( θ ) and add the height of your eyes to get the tower’s height.
Example: At 50 feet from the base of the tower, the angle to the top is 40 degrees. If my eyes are 5.5 feet above the ground, the tower height = (50 x tan(40)) + 5.5 = (50 x 0.84) + 5.5 = 47.5 feet.
Trig pro tip: If you move away from the tower until the angle is 45 degrees, then the tower height is equal to the distance from the tower + the height of your eyes. No calculation required!
And let’s get the Pythagorean Theorem in there too, shall we? If you know both the height of a tree or tower and the distance from the base, the length of whatever is stretched between those two points—a guy wire, an antenna, or a rope—is equal to:
Length = square root of (height squared + distance squared)
Note that if you aren’t using the “radical” that looks like √ it is common to use “sqrt” with whatever is to have its square root calculated in parentheses as shown in the following example:
Example: How much guy wire is needed between the top of a 90-foot tower and a guy anchor point 100 feet away from the tower? Length = sqrt (902 + 1002) = sqrt (8100 + 10000) = 134.5 feet. Don’t forget to account for the extra length required to attach to insulators and anchor points!

